剪断応力とは、「ずれに伴い、材料の横断面に、互いに平行で向きが逆に生ずる応力」であり、下図におけるτがその力です。
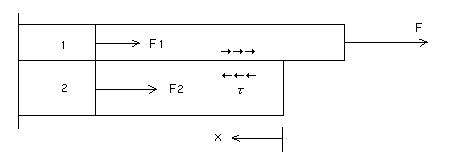
今、横断面1においては、剪断応力によって力の大きさが右から左にFからF1に軽減され、横断面2においては、剪断応力によって力の大きさが右から左に0からF2に増やされています。これは、各点における剪断応力の和によるものです。
この課題は皆さんに簡単なプログラミングの練習を行ってもらうためのものです.
剪断応力とは、「ずれに伴い、材料の横断面に、互いに平行で向きが逆に生ずる応力」であり、下図におけるτがその力です。

今、横断面1においては、剪断応力によって力の大きさが右から左にFからF1に軽減され、横断面2においては、剪断応力によって力の大きさが右から左に0からF2に増やされています。これは、各点における剪断応力の和によるものです。
それでは、この剪断応力をグラフにしてみましょう。
さて、この課題を解くのにまず必要なこととして式を定義する事が挙げられます。式を定義するには、
(xの後の下線(アンダーバー:Shiftキーを押しながら右シフトキーのすぐ左のキー)に注意しましょう)
例えば 、f(x)=5xを定義したいときは、
f[x_] := 5*x
とすればよいのです。
また,x=tでの値(#)を定めるには
とします。
いまの場合、下記 g(x) の a,b,c に適当な数値をいれてやって定義しましょう。
今、X軸を図のように (xの初期値は2) とった時に剪断応力g(x)は、
と表す事が出来ます。この式では新たなg(x)を定義するために,それ以前のg(k)(k=1,2,・・,x-1)を使っていますね.専門的には再帰的定義と呼びます.Mathematicaでは再帰的定義が許されています.この場合、xの初期値はMathematicaで計算しやすいように2にしています。
この場合、一番右端の点 (x=2) で剪断応力は最大となり、値は ab となりますね。
では、Mathematicaを使ってみましょう。
Mathematicaの場合、ΣではなくSumを用います。
で、g(k)のkが1からkmaxまでを足し合わせたものを表します。積算範囲が1からではない場合には,{k,kmin,kmax}のように表現します.
それでは、g(x)を実際に計算して点で表してみましょう。そのためにはTableを用います。
で、式g(x)を繰り返し計算して結果をリストの形で表すことが出来ます。
この場合では、minはもちろん初期値の2で、minとmaxとの間隔は10くらい取れば十分でしょう。
あとは、出て来たリストをプロットしてやればOKです。初めのa,b,cの取り方次第でグラフの形が変わってきますが,この課題では実際の数値を与えていないので、妥当な結果を得るために何度か計算しなおす必要があるでしょう.不安定な解は力が負になったりの非現実的な条件設定になっている可能性があります。
この結果から剪断応力のもっとも大きい部分は、接合の初めの部分であることがわかります。実際、人工骨や歯などでもっとも剥がれたり壊れやすい部分は、こういった継ぎ目の部分です。また,剪断応力は骨などの固体だけでなく,血液などの流体中や血管壁との境界面にも存在します.血管中に挿入したカテーテルなどの異物の付近では,血流が乱れて剪断応力が発生し,赤血球が壊されるなどして血栓が生じます.その他,アテローム性動脈硬化などにも血管壁の剪断応力が関係します.